Making repeated addition faster

In the previous Learning Outcome, we experienced why addition cannot offer an advantage to repeated addition of the same numbers; addition operates vertically and place value by place value. Indeed, we need to think beyond any modifications in the addition process to get a quicker sum of the same numbers.
Let us discover what kind of a new process would help get a quicker ‘sum’ of the same numbers. We will use smaller numbers to discover some new insights in addition of the same numbers to make it easier to work with. The lessons learnt from working with smaller numbers will be equally applicable to any other numbers; that is the nature of the decimal number system.
Consider the following statement of addition sum of same numbers:
2 + 2 + 2 + 2 + 2
Let us ‘quantify the numbers’ and assume that each 2 represents a pair of tennis balls (anyway, all the numbers must have like units to be addable). There will be 5 addends, each of 2 things, and the things they represent is tennis balls. Thus, the given expression becomes – 2 balls + 2 balls + 2 balls + 2 balls + 2 balls – and it can be shown pictorially as:

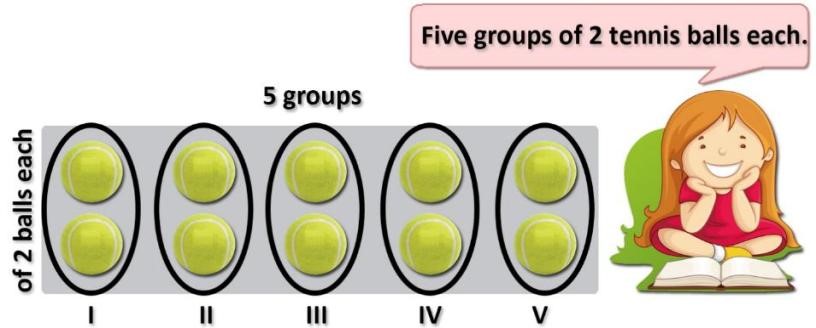
The picture of balls can be considered as 5 groups of 2 balls! Thus, the following three equalities hold:
2 + 2 + 2 + 2 + 2 = 2 balls + 2 balls + 2 balls + 2 balls + 2 balls = 5 groups of 2 balls.
‘5 groups of 2 balls (each)’ literally captures the fact of ‘2 balls + 2 balls + 2 balls + 2 balls + 2 balls’; the two are equivalent statements - ‘5 groups of 2 balls (each)’ and ‘2 balls + 2 balls + 2 balls + 2 balls + 2 balls’ – both expressing the quantity 10 (balls) in total.

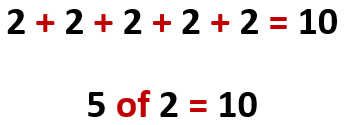
‘Of ‘as a proposition in English language very precisely express multiple same quantities.
This ability to express an addition expression into a concise, equivalent statement in a natural language is a giant leap in logic and knowledge. We will explore this more as we progress in the book. The essence of repeated addition is in this translation of an addition expression into a very brief, equivalent statement in English.
Let us discuss a couple of more examples of visualising and expressing repeated addition expressions in their equivalent English expressions.

Example 1
What does the following expression of sum of same number: 4 + 4 + 4 + 4 + 4 + 4 + 4, represent? Let us ‘quantify the numbers’ and assume that each 4 represents a group of kids. We assume that the kids are all similar in some same ways since we have grouped them. There are 7 addends, each of 4 kids (each addend represents 4 kids). Our given expression becomes – 4 kids + 4 kids + 4 kids + 4 kids + 4 kids + +4 kids + 4 kids.
The expression 4 + 4 + 4 + 4 + 4 + 4 + 4 = 4 kids + 4 kids + 4 kids + 4 kids + 4 kids + 4 kids + 4 kids = 7 groups of 4 kids.
‘7 groups of 4 kids (each)’ literally captures the fact of ’4 kids + 4 kids + 4 kids + 4 kids + 4 kids + 4 kids + 4 kids’. The two are equivalent statements - ‘7 groups of 4 kids (each)’ and ‘4 kids + 4 kids + 4 kids + 4 kids + 4 kids + 4 kids + 4 kids’ – both expressing the quantity 28 kids in total.

Example 2
Consider the expression of the sum of the same number: 12 + 12 + 12 + 12 + 12. Let us ‘quantify the numbers’ and assume that each 12 represents a dozen eggs. There are be 5 addends, each of 12 eggs; each addend represents a dozen eggs. Thus, the given expression becomes – 12 eggs + 12 eggs + 12 eggs + 12 eggs + 12 eggs.
And, 12 + 12 + 12 + 12 + 12 = 12 eggs + 12 eggs + 12 eggs + 12 eggs + 12 eggs = 5 groups of 12 eggs.
‘5 groups of 12 eggs (each)’ literally captures the fact of ‘12 eggs + 12 eggs + 12 eggs + 12 eggs + 12 eggs’; the two are equivalent statements - ‘5 groups of 12 eggs (each)’ and ‘12 eggs + 12 eggs + 12 eggs + 12 eggs + 12 eggs’ – both expressing the quantity 60 (eggs) in total.
Repeated addition expressions of the same number/ quantity can be written in much briefer expression in any language of communication. In English, the preposition ‘of’ comprehensively captures the essence of repeated addition of the same quantity number. Incidentally, the preposition ‘of’ to talk of multiple quantities of the same thing is very frequent in everyday conversations.
In the next Learning Outcome, we will explore the everyday usages of the preposition ‘of’ to see if it can represent all situations of repeated addition of the same thing. 

Summary

Excerpted from the book ‘Foundations of Multiplication (Mathematics as a language)’ by Sandeep Srivastava and Saloni Srivastava